Matematyka analizy tensorów

Analiza tensorowa, gałąź matematyki związana z relacjami lub prawami, które pozostają ważne bez względu na układ współrzędnych stosowany do określania wielkości. Takie relacje nazywa się kowariantem. Tensory zostały wynalezione jako rozszerzenie wektorów w celu sformalizowania manipulacji elementami geometrycznymi powstającymi w badaniu rozmaitości matematycznych.

Wektor jest bytem, ​​który ma zarówno wielkość, jak i kierunek; jest reprezentowany przez rysunek strzałki i łączy się z podobnymi bytami zgodnie z prawem równoległoboku. Z powodu tego prawa wektor ma komponenty - inny zestaw dla każdego układu współrzędnych. Po zmianie układu współrzędnych elementy wektora zmieniają się zgodnie z matematycznym prawem transformacji, które można wywnioskować z prawa równoległoboku. To prawo transformacji komponentów ma dwie ważne właściwości. Po pierwsze, po sekwencji zmian, które kończą się w oryginalnym układzie współrzędnych, elementy wektora będą takie same jak na początku. Po drugie, zależności między wektorami - na przykład trzy wektory U, V, W, tak że 2U + 5 V = 4 W - będą obecne w komponentach niezależnie od układu współrzędnych.

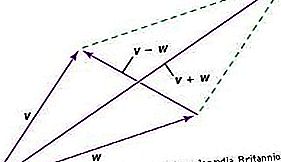
Wektor można zatem traktować jako byt, który w n-wymiarowej przestrzeni ma n składników, które przekształcają się zgodnie ze szczególnym prawem transformacji posiadającym powyższe właściwości. Sam wektor jest bytem obiektywnym niezależnym od współrzędnych, ale jest traktowany w kategoriach komponentów ze wszystkimi układami współrzędnych na równych prawach.

Bez nalegania na obrazowy obraz, tensor definiuje się jako obiektywny byt posiadający komponenty, które zmieniają się zgodnie z prawem transformacji, które jest uogólnieniem wektorowego prawa transformacji, ale które zachowuje dwie kluczowe właściwości tego prawa. Dla wygody współrzędne są zwykle ponumerowane od 1 do n, a każdy element tensora jest oznaczony literą zawierającą indeks górny i dolny, z których każdy niezależnie przyjmuje wartości od 1 do n. Zatem tensor reprezentowany przez składowe T ^ab _c miałby n ³ składowych, ponieważ wartości a, b i c przebiegałyby od 1 do n. Skalary i wektory stanowią szczególne przypadki tensorów, z których pierwszy ma tylko jeden element na układ współrzędnych, a drugi n. Każda liniowa zależność między składowymi tensora, taka jak 7R ^a _bcd + 2S ^a _bcd - 3T ^a _bcd = 0, jeśli jest ważna w jednym układzie współrzędnych, jest ważna we wszystkich, a zatem reprezentuje relację, która jest obiektywna i niezależna od układów współrzędnych pomimo brak obrazowej reprezentacji.

Szczególnie interesujące są dwa tensory, zwane tensorem metrycznym i tensorem krzywizny. Tensor metryczny jest wykorzystywany na przykład do przekształcania elementów wektora w wielkości wektorów. Dla uproszczenia rozważ przypadek dwuwymiarowy z prostymi współrzędnymi prostopadłymi. Niech wektor V będzie miał składowe V ₁, V ₂. Następnie przez twierdzenie Pitagorasa zastosowane do prawego trójkąta OAP kwadrat wielkości V jest określony przezOP ² = (V ₁) ² + (V ₂) ².

W tym równaniu ukryty jest tensor metryczny. Jest ukryty, ponieważ tutaj składa się z zer i jedynek, które nie są wpisane. Jeśli równanie zostanie przepisane w postaci OP ² = 1 (V ₁) ² + 0V ₁ V ₂ + 0V ₂ V ₁ + 1 (V ₂) ², widoczny jest pełny zestaw elementów (1, 0, 0, 1) tensora metrycznego. W przypadku zastosowania współrzędnych ukośnych wzór na OP ² przyjmuje bardziej ogólną postać OP ² = g ₁₁ (V ₁) ² + g ₁₂ V ₁ V ₂ + g ₂₁ V ₂ V ₁ + g ₂₂ (V ₂) ², ilości g ₁₁, g ₁₂, g ₂₁, g ₂₂ są nowymi składnikami tensora metrycznego.

Z tensora metrycznego można zbudować skomplikowany tensor, zwany tensorem krzywizny, który reprezentuje różne aspekty wewnętrznej krzywizny przestrzeni n-wymiarowej, do której należy.

Tensory mają wiele zastosowań w geometrii i fizyce. Tworząc swoją ogólną teorię względności, Albert Einstein argumentował, że prawa fizyki muszą być takie same bez względu na stosowany układ współrzędnych. Doprowadziło go to do wyrażenia tych praw w postaci równań tensorowych. Z jego specjalnej teorii względności wiadomo było już, że czas i przestrzeń są tak ściśle ze sobą powiązane, że tworzą niepodzielną czterowymiarową czasoprzestrzeń. Einstein postulował, że grawitacja powinna być reprezentowana wyłącznie w kategoriach metrycznego tensora czterowymiarowej czasoprzestrzeni. Aby wyrazić relatywistyczne prawo grawitacji, miał on jako elementy składowe tensor metryczny i utworzony z niego tensor krzywizny. Kiedy postanowił ograniczyć się do tych elementów, ich bardzo ubóstwo doprowadziło go do zasadniczo unikatowego równania tensorowego dla prawa grawitacji, w którym grawitacja pojawiła się nie jako siła, ale jako przejaw krzywizny czasoprzestrzeni.

Chociaż tensory były badane wcześniej, to sukces ogólnej teorii względności Einsteina spowodował powszechne zainteresowanie matematyków i fizyków tensorami i ich zastosowaniami.