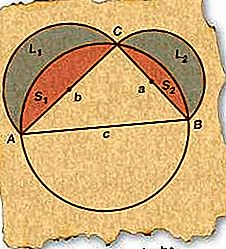
Hipokrates z Chios (fl. Ok. 460 pne) wykazał, że obszary w kształcie księżyca między łukami kołowymi, znane jako lunes, można wyrazić dokładnie jako obszar prostoliniowy lub kwadraturę. W poniższym prostym przypadku dwie krawędzie rozwinięte wokół boków prawego trójkąta mają łączną powierzchnię równą powierzchni trójkąta.
-
Zaczynając od prawej ABABC, narysuj okrąg, którego średnica pokrywa się z AB (strona c), przeciwprostokątną. Ponieważ każdy prawy trójkąt narysowany ze średnicą koła dla jego przeciwprostokątnej musi być wpisany w koło, C musi znajdować się na okręgu.
-
Narysuj półkola o średnicach AC (strona b) i BC (strona a) jak na rysunku.
-
Oznacz otrzymane linie L 1 i L 2 oraz powstałe segmenty S 1 i S 2, jak pokazano na rysunku.
-
Teraz suma wiązek (L 1 i L 2) musi być równa sumie półkoli (L 1 + S 1 i L 2 + S 2) zawierających je minus dwa segmenty (S 1 i S 2). Zatem L 1 + L 2 = π / 2 (b / 2) 2 - S 1 + π / 2 (a / 2) 2 - S 2 (ponieważ powierzchnia koła jest π razy kwadrat promienia).
-
Suma segmentów (S 1 i S 2) równa się powierzchni półkola na podstawie AB minus powierzchnia trójkąta. Zatem S 1 + S 2 = π / 2 (c / 2) 2 - ΔABC.
-
Podstawiając wyrażenie z kroku 5 do kroku 4 i uwzględniając wspólne terminy, L 1 + L 2 = π / 8 (a 2 + b 2 - c 2) + ΔABC.
-
Ponieważ ∠ACB = 90 °, a 2 + b 2 - c 2 = 0, według twierdzenia Pitagorasa. Zatem L 1 + L 2 = ΔABC.
Hipokratesowi udało się wyrównać kilka rodzajów lun, niektóre na łukach większych i mniejszych niż półkole, i zasugerował, choć może nie wierzył, że jego metoda może obrócić cały okrąg. Pod koniec epoki klasycznej Boecjusz (ok. 470–524), którego łacińskie tłumaczenia fragmentów Euklidesa utrzymywałoby światło geometrii migoczące przez pół tysiąclecia, wspomniał, że ktoś osiągnął kwadrat. Nie wiadomo, czy nieznany geniusz zastosował śliwki, czy inną metodę, ponieważ z powodu braku miejsca Boecjusz nie dał demonstracji. W ten sposób przekazał wyzwanie kwadratury koła wraz z fragmentami geometrii najwyraźniej przydatnymi do jego wykonania. Europejczycy trzymali się tego nieszczęsnego zadania również w Oświeceniu. Wreszcie w 1775 r. Paryska akademia nauk, mająca dość dostrzeżenia błędów w wielu przedstawionych jej rozwiązaniach, odmówiła dalszego zajmowania się kwadratowymi kwadratami.